《算法》笔记：第2章 排序

Posted on Edited on In

《算法》第2章：排序。

初级排序算法，归并排序，快速排序，优先队列，应用。

在计算时代早期，普遍认为30%的计算周期都用在了排序上。如果今天这个比例降低了，可能的原因之一是排序算法更高效了，而并非排序的重要性降低了。

2.1 初级排序算法

学习两种初级的排序算法以及其中一种的变体。这些简单的算法在某些情况下比我们以后讨论的复杂算法更有效。

2.1.1 游戏规则

比较函数的模板。

1
2
3
4
5
6
7
func less(v, w int) bool {
	return v < w
}

func exch(a []int, i, j int) {
	a[i], a[j] = a[j], a[i]
}

对于每一种排序，都需要验证是否排序成功，运行时间和额外的内存使用。

2.1.2 选择排序

对于长度为N的数组，选择排序需要大约(N^2 / 2)次比较和N次交换。选择排序有两个鲜明的特点：

  • 运行时间和输入无关。总是需要那么多次比较，无论输入的数组已经有序或全部相等或随机排列的。
  • 数据移动的次数最少。只需要N次交换。
1
2
3
4
5
6
7
8
9
10
11
12
func SelectionSort(a []int) {
	length := len(a)
	for i := 0; i < length-1; i++ {
		min := i
		for j := i+1; j < length; j++ {
			if a[j] < a[min] {
				min = j
			}
		}
		exch(a, min, i)
	}
}

2.1.3 插入排序

对于随机排列的长度为N且主键不重复的数组：

  • 平均，需要(N^2 / 4)次比较以及(N^2 / 4)次交换。
  • 最坏情况下，需要(N^2 / 2)次比较以及(N^2 / 2)次交换。
  • 最好情况下，需要N-1次比较和0次交换。

特点：

  • 插入排序所需的时间取决于输入中元素的初始顺序。
  • 插入排序对实际应用中常见的某类非随机数组很有效。
  • 插入排序对部分有序的数组很有效。典型的部分有序的数组：
    • 数组中每个元素距离它最终位置都不远。
    • 一个有序的大数组接一个小数组。
    • 数组中只有几个元素的位置不正确。
1
2
3
4
5
6
7
8
9
10
func InsertionSort(a []int) {
	length := len(a)
	for i := 1; i < length; i++ {
		for j := i; j >= 0; j-- {
			if a[j] < a[j-1] {
				exch(a, j, j-1)
			}
		}
	}
}

2.1.4 排序算法的可视化

数据结构和算法动态可视化 (Chinese) - VisuAlgo

2.1.5 比较两种排序算法

  1. 对于随机排序的无重复主键的数组，插入排序和选择排序的运行时间是平方级别的，两者之比应该是一个较小的常数。
  2. 某些特殊情况下它们也是很好的选择。

2.1.6 希尔排序

希尔排序的思想是使数组中任意间隔为h的元素都是有序的，称为h有序数组。

希尔排序更高效的原因是它权衡了子数组的规模和有序性。排序之初，各个子数组都很短；排序之后，子数组部分有序。这两种情况都很适合插入排序。

希尔排序也可以用于大型数组，它对任意排序的数组表现也很好。希尔排序比插入排序和选择排序快得多，并且数组越大，优势越大。

希尔排序的时间复杂度，目前最重要的结论是它的运行时间达不到平方级别。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
func ShellSort(a []int) {
	length := len(a)
	h := 1
	for h < length / 3 {
		h = h * 3 + 1
	}
	for h >= 1 {
		for i := h; i < length; i++ {
			for j := i; j >= h; j -= h {
				if less(a, j, j-h) {
					exch(a, j, j-h)
				}
			}
		}
		h /= 3
	}
}

2.2 归并排序

归并操作：将两个有序的数组归并成一个更大的有序数组。

归并排序：分成两部分，分别排序，然后归并起来。

归并排序最吸引人的性质是它能够保证将长度为N的数组排序所需的时间和NlogN成正比；它的主要缺点是它所需的额外空间和N成正比。

2.2.1 原地归并的抽象方法

将两个有序的数组归并成一个更大的有序数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
// 归并a和b两个切片
func merge1(a, b []int) []int {
	ret := make([]int, 0)
	for len(a) > 0 && len(b) > 0 {
		if a[0] > b[0] {
			ret = append(ret, b[0])
			b = b[1:]
		} else {
			ret = append(ret, a[0])
			a = a[1:]
		}
	}
	for len(a) > 0 {
		ret = append(ret, a[0])
		a = a[1:]
	}
	for len(b) > 0 {
		ret = append(ret, b[0])
		b = b[1:]
	}
	return ret
}

// 归并[low:mid]和[mid+1:hig]
func merge2(a []int, low, mid, hig int) {
	i, j := low, mid+1
	aux := make([]int, 0)
	for _, v := range a {
		aux = append(aux, v)
	}
	for k := low; k <= hig; k++ {
		if i > mid {
			a[k] = aux[j]
			j++
		} else if j > hig {
			a[k] = aux[i]
			i++
		} else if less(a, i, j) {
			a[k] = aux[i]
			i++
		} else {
			a[k] = aux[j]
			j++
		}
	}
}

2.2.2 自顶向下的归并排序

应用了高效算法设计的分治思想。如果它能将两个子数组排序，它就能够通过归并两个子数组来将整个数组排序。

  • 对于长度为N的任意数组，自顶向下的归并排序需要0.5NlgN到NlgN次比较。
  • 对于长度为N的任意数组，自顶向下的归并排序最多需要访问数组6NlgN次。

归并排序的主要缺点是额外空间和N大小成正比，另一方面，通过一些改变能够大幅度缩短归并排序的运行时间。

  • 对小规模子数组使用插入排序。递归会使小规模问题的方法调用过于频繁。
  • 不将元素复制到辅助数组。可以节省时间，但是空间不行。
1
2
3
4
5
6
7
8
func MergeSortTop2Bottom(a []int) []int {
	length := len(a)
	if length <= 1 {
		return a
	}
	mid := length / 2
	return merge1(MergeSortTop2Bottom(a[:mid]), MergeSortTop2Bottom(a[mid:]))
}

2.2.3 自底向上的归并排序

对于长度为N的任意数组，自顶向下的归并排序需要0.5NlgN到NlgN次比较，最多需要访问数组6NlgN次。

1
2
3
4
5
6
7
8
func MergeSortBottom2Top(a []int) {
	length := len(a)
	for sz := 1; sz < length; sz += sz {
		for low := 0; low < length-sz; low += sz+sz {
			merge2(a, low, low+sz-1, min(low+sz+sz-1, length-1))
		}
	}
}

2.2.4 排序算法的复杂度

没有任何基于比较的算法能够保证使用少于lg(N!)~NlgN次比较，将长度为N的数组排序。

归并排序是一种渐进最优的基于比较排序的算法。

渐进最优性

2.3 快速排序

应用最广泛的算法，流行的原因是它实现简单、适用于各种不同的输入数据且在一般应用中比其他排序算法都要快得多。

快速排序的特点：

  • 原地排序。只需要一个很小的辅助栈。
  • 长度为N的数组所需的时间和NlgN成正比。
  • 快速排序的内循环比大多数排序算法都要短小，意味着它无论在理论上还是实际中都要更快。
  • 缺点是非常脆弱，要小心避免低劣的性能。

2.3.1 基本算法

快排是一种分治的排序算法，分成两个子数组，两部分独立地排序。注意：

  • 别越界，测试条件要注意；
  • 保持随机性，可以在排序前打乱数组；
  • 终止递归的条件。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
func QuickSort(a []int) {
	quickSort(a, 0, len(a)-1)
}

func quickSort(a []int, left, right int) {
	if left >= right {
		return
	}
	i, j := left, right
	key := a[left]
	for left < right {
		for left < right && a[right] >= key {
			right--
		}
		if left < right {
			a[left] = a[right]
			left++
		}
		for left < right && a[left] <= key {
			left++
		}
		if left < right {
			a[right] = a[left]
			right--
		}
	}
	a[left] = key
	quickSort(a, i, left-1)
	quickSort(a, left+1, j)
}

2.3.2 性能特点

平均需要~2NlnN次比较，以及1/6次交换。最多需要N^2/2次比较，但随机打乱能预防这种情况。

快排的实现仍有一个潜在的缺点：在切分不平衡时这个程序可能会及其低效。

2.3.3 算法改进

  1. 切换到插入排序：和大多数递归排序算法一样，改进快排的性能一个简单的办法。
  2. 三取样切分：使用子数组的一小部分元素的中位数来切分数组。
  3. 熵最优的排序：含有大量元素相同的时候，将数组切分成三部分，分别对应小于等于大于。

2.4 优先队列

许多应用都需要处理有序的元素，但不一定要求全部有序，或者不一定要一次就将它们排序。很多情况下我们会收集一些元素，处理当前键值最大的元素，然后再收集更多的元素，再处理。

在这种情况下，合适的数据结构要支持两种操作：删除最大的元素和插入元素。这种数据结构叫优先队列。

2.4.1 API

最重要的操作时删除最大元素和插入元素。

MaxPQ
Insert(item) 插入
max() 返回最大元素
delMax() 删除最大元素
isEmpty()
size()

从N个输入中找到最大的M个元素所需的成本：

示例 时间 空间
排序算法 NlgN N
初级实现的优先队列 NM M
基于堆实现的优先队列 NlogM M

2.4.2 初级实现

2.4.2.1 数组实现（无序）

基于下压栈的代码。

insert()使用push()。

要删除最大元素，可以添加一段类似于选择排序的内循环代码，将最大的元素和边界元素交换然后删除它。

2.4.2.2 数组实现（有序）

insert()方法，添加时使用插入排序。

删除最大元素和pop()一样。

2.4.2.3 链表表示法

跟基于链表实现的下压栈类似。

使用无序链表是解决这个问题的惰性方法，仅在必要时才会找出最大元素；

使用有序链表是积极方法，尽可能在插入元素的时候保持列表有序，使后续操作更高效。

2.4.3 堆的定义

实现栈或队列，和实现优先队列的最大不同在于性能的要求。对于栈和队列，能在常数时间完成所有操作；对于优先队列，插入元素和删除最大元素两个操作之一在最坏情况下需要线性时间来完成。基于堆来实现可以保证这两种操作都能更快运行。

堆的定义和性质如下：

  • 当一棵二叉树的每个结点都大于等于它的两个子结点时，它被称为堆有序。

  • 根节点是堆排序的二叉树中最大的结点。

  • 二叉堆是一组能够用堆有序的完全二叉树排序的元素，并在数组中按照层级储存。

  • k位置的结点，它的父节点位置为k-1/2，子结点分别为2k+1和2k+2。

  • 一棵大小为N的完全二叉树的高度为floor(lgN)。

2.4.4 堆的算法

对于大小为N的优先队列，插入操作只需不超过lgN+1次比较，删除操作需要不超过2lgN次比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
type MaxPriorityQueue struct {
	priorityQueue []int
	length int
}

func (pq *MaxPriorityQueue) IsEmpty() bool {
	return pq.length == 0
}

func (pq *MaxPriorityQueue) Size() int {
	return pq.length
}

// 上浮，在插入操作之后
func (pq *MaxPriorityQueue) swim(k int) {
	for k > 0 && less(pq.priorityQueue, k-1/2, k) {
		exch(pq.priorityQueue, k-1/2, k)
		k = k-1 / 2
	}
}

//下沉，恢复堆
func (pq *MaxPriorityQueue) sink(k int) {
	for 2*k+1 < pq.length {
		j := 2*k + 1
		if j+1 < pq.length && less(pq.priorityQueue, j, j+1) {
			j++
		}
		if !less(pq.priorityQueue, k, j) {
			break
		}
		exch(pq.priorityQueue, k, j)
		k = j
	}
}

func (pq *MaxPriorityQueue) Insert(item int) {
	pq.priorityQueue[pq.length] = item
	pq.swim(pq.length)
	pq.length++
}

func (pq *MaxPriorityQueue) DelMax() int {
	max := pq.priorityQueue[0]
	exch(pq.priorityQueue, 0, pq.length-1)
	pq.length--
	pq.priorityQueue = pq.priorityQueue[:pq.length]
	pq.sink(0)
	return max
}

2.4.5 堆排序

下沉操作：只需要少于2N次比较和少于N次的交换。

排序操作：只需要少于2NlgN+2N次比较。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
func HeapSort(a []int) {
	// 构建最大堆
	for i := len(a)/2 - 1; i >= 0; i-- {
		AdjustHeap(a, i, len(a))
	}
	// 置于队尾
	for j := len(a) - 1; j > 0; j-- {
		a[0], a[j] = a[j], a[0]
		AdjustHeap(a, 0, j)
	}
}

func AdjustHeap(a []int, i, length int) {
	tmp := a[i]
	for k := i*2 + 1; k < length; k = k*2 + 1 {
		if k+1 < length && a[k] < a[k+1] {
			k++
		}
		if a[k] > tmp {
			a[i] = a[k]
			i = k
		} else {
			break
		}
	}
	a[i] = tmp
}

2.5 应用

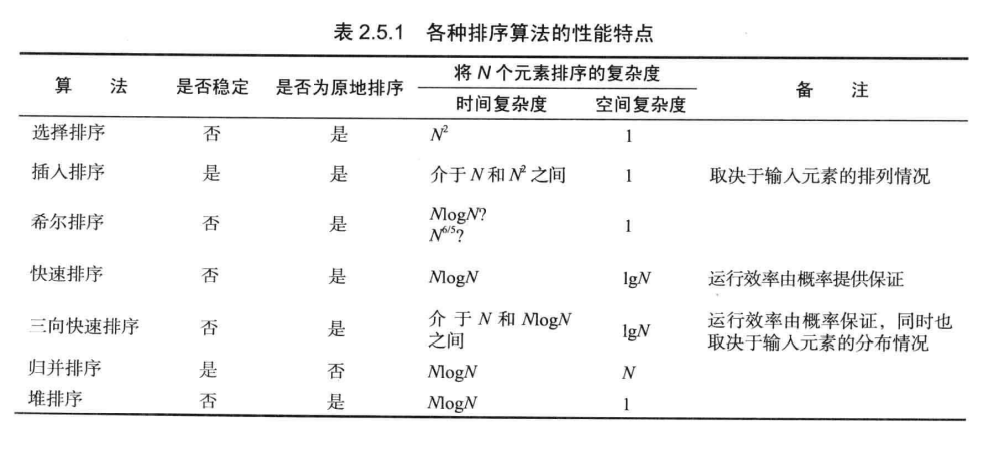
快速排序是最快的通用排序算法。