《算法》笔记：第4章 图

Posted on Edited on In

《算法》第4章：图。

无向图，有向图，最小生成树，最短路径。

4种最重要的图模型：无向图（简单链接）、有向图（方向性）、加权图（带有权值）和加权有向图（既有方向性又带有权值）。

4.1 无向图

  • 使用0至V-1来表示一张含有V个顶点各个顶点；

  • v-w表示连接v和w的边；

  • 特殊的图：含有平行边的称为多重图，没有平行边或自环的称为简单图。

    • 自环：一条连接到自己的边。
    • 平行边：同一对顶点的边。

4.1.1 术语表

和图相关的术语很多：

  • 相邻：两个顶点通过一条边相连。
  • 度数：依附顶点的边的条数。
  • 子图：由一幅图的所有边的一个子集组成的图。
  • 路径：由边顺序连接的一系列顶点。
    • 简单路径：没有重复顶点的路径。
    • 环：起点和终点相同。
    • 简单环：除起点和终点之外没有重复顶点和边。
    • 长度：所包含的边数。
  • 连通图：任意一个顶点都能到达另一个顶点。
  • 无环图：没有环。
  • 树：无环连通图。
    • 森林：互不相连的树组成的集合。
    • 生成树：连通图的生成树是它的一副子图，含有图中所有顶点且是一棵树。
  • 二分图：将所有结点分为两部分的图。

4.1.2 表示无向图的数据类型

最常用的图处理算法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
func Degree(g Graph, v int) int {
	return len(g.Adj(v))
}

func MaxDegree(g Graph) int {
	max := 0
	for i :=0; i < g.V; i++ {
		if d := Degree(g, i); d > max {
			max = d
		}
	}
	return max
}

func AvgDegree(graph Graph) float64 {
	return 2.0 * float64(graph.E) / float64(graph.V)
}

func NOfSelfLoops(graph Graph) int {
	count := 0
	for v := 0; v < graph.V; v++ {
		for _, w := range graph.Adj(v) {
			if w == v {
				count++
			}
		}
	}
	return count / 2
}

func ToString(g Graph) string {
	s := fmt.Sprintf("%v vertices, %v edges\n", g.V, g.E)
	for v := 0; v < g.V; v++ {
		s += fmt.Sprintf("%v: ", v)
		for _, w := range g.Adj(v) {
			s += fmt.Sprintf("%v ", w)
		}
		s += "\n"
	}
	return s
}

Graph数据类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
type Graph struct {
	V int
	E int
	adj []Chapter01Foundation.ListBag
}

func NewGraph(v int) *Graph {
	 return &Graph{
		V: v,
		E: 0,
		adj: make([]Chapter01Foundation.ListBag, v),
	}
}

func (g *Graph) AddEdge(v, w int) {
	g.adj[v].Add(w)
	g.adj[w].Add(v)
	g.E++
}

func (g *Graph) Adj(v int) []interface{} {
	return g.adj[v].Iterator()
}

4.1.3 深度优先搜索

跟路径相关，需要使用深度优先搜索。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
type DepthFirstSearch struct {
	marked []bool
	count int
}

func NewDepthFirstSearch(g Graph, s int) *DepthFirstSearch {
	d := new(DepthFirstSearch)
	d.count = 0
	d.marked = make([]bool, g.V)
	d.DFS(g, s)
	return d
}

func (d *DepthFirstSearch) DFS(g Graph, v int) {
	d.marked[v] = true
	d.count++
	for _, w := range g.Adj(v) {
		if !d.marked[w.(int)] {
			d.DFS(g, w.(int))
		}
	}
}

4.1.4 寻找路径

单点路径：给定一幅图和一个起点，到目的顶点是否存在一条路径，找出这条路径。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
// 是否有一条路径
type DepthFirstPaths struct {
	marked []bool	//这个顶点上调用过DFS吗？
	edgeTo []int	//从起点到一个顶点的已知路径上的最后一个顶点
	s int			//起点
}

func NewDepthFirstPaths(g Graph, start int) *DepthFirstPaths {
	p := new(DepthFirstPaths)
	p.marked = make([]bool, g.V)
	p.edgeTo = make([]int, g.V)
	p.s = start
	p.DFS(g, start)
	return p
}

func (p *DepthFirstPaths) DFS(g Graph, v int) {
	p.marked[v] = true
	for _, w := range g.Adj(v) {
		if !p.marked[w.(int)] {
			p.edgeTo[w.(int)] = v
			p.DFS(g, w.(int))
		}
	}
}

func (p *DepthFirstPaths) HasPathTo(v int) bool {
	return p.marked[v]
}

func (p *DepthFirstPaths) PathTo(v int) []int {
	if !p.HasPathTo(v) {
		return nil
	}
	ret := make([]int, 0)
	for x := v; x != p.s; x = p.edgeTo[x] {
		ret = append(ret, x)
	}
	ret = append(ret, p.s)
	return ret
}

4.1.5 广度优先搜索

处理最短路径的方法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
type BreadthFirstPaths struct {
	marked []bool
	edgeTo []int
	start int
}

func NewBreadthFirstPaths(g Graph, s int) *BreadthFirstPaths {
	ret := new(BreadthFirstPaths)
	ret.marked = make([]bool, g.V)
	ret.edgeTo = make([]int, g.V)
	ret.start = s
	ret.BFS(g, s)
	return ret
}

func (p *BreadthFirstPaths) BFS(g Graph, s int) {
	l := list.New()
	p.marked[s] = true
	l.PushBack(s)
	for l.Len() != 0 {
		v := l.Remove(l.Front()).(int)
		for _, wRow := range g.Adj(v) {
			w := wRow.(int)
			if !p.marked[w] {
				p.edgeTo[w] = v
				p.marked[w] = true
				l.PushBack(w)
			}
		}
	}
}

func (p *BreadthFirstPaths) HasPathTo(v int) bool {
	return p.marked[v]
}

func (p *BreadthFirstPaths) PathTo(v int) []int {
	if !p.HasPathTo(v) {
		return nil
	}
	ret := make([]int, 0)
	for x := v; x != p.start; x = p.edgeTo[x] {
		ret = append(ret, x)
	}
	ret = append(ret, p.start)
	return ret
}

4.1.6 连通分量

一个图的极大连通子图称为连通分量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
type CC struct {
	marked []bool	
	id []int	//连通分量的编号
	count int	//当前编号
}

func NewCC(g Graph) *CC {
	ret := new(CC)
	ret.marked = make([]bool, g.V)
	ret.count = 0
	ret.id = make([]int, g.V)
	for s := 0; s < g.V; s++ {
		if !ret.marked[s] {
			ret.DFS(g, s)
			ret.count++
		}
	}
	return ret
}

func (cc *CC) DFS(g Graph, v int) {
	cc.marked[v] = true
	cc.id[v] = cc.count
	for _, wRow := range g.Adj(v) {
		w := wRow.(int)
		if !cc.marked[w] {
			cc.DFS(g, w)
		}
	}
}

func (cc *CC) Connected(v, w int) bool {
	return cc.id[v] == cc.id[w]
}

使用深度优先算法处理图的其他实例

4.1.7 符号图

使用字符串而非整数来表示和指代顶点。

书上的方法是，使用两个数组，一个对于索引->字符串，一个从字符串->索引。然后图还是使用整数表示顶点。

我用了一个map记录。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
type SymbolGraph struct {
	// 键为图的顶点，值为顶点的整数表示
	// 值为0时，表示顶点不存在，从1开始计算。
	index map[string]int
	graph *Graph
}

func NewSymbolGraph(filePath string) *SymbolGraph {
	sg := new(SymbolGraph)
	sg.index = make(map[string]int)
	file, err := os.Open(filePath)
	if err != nil {
		fmt.Println("open error")
		return nil
	}
	defer file.Close()
	count := 1
	br := bufio.NewReader(file)
	for {
		row, _, c := br.ReadLine()
		if c == io.EOF {
			break
		}
		data := string(row)
		splits := strings.Split(data, " ")
		for _, v := range splits {
			if sg.index[v] == 0 {
				sg.index[v] = count
				count++
			}
		}
	}
	sg.graph = NewGraph(count-1)
	br = bufio.NewReader(file)
	for {
		row, _, c := br.ReadLine()
		if c == io.EOF {
			break
		}
		data := string(row)
		splits := strings.Split(data, " ")
		v := sg.index[splits[0]] - 1
		w := sg.index[splits[1]] - 1
		sg.graph.AddEdge(v, w)
	}
	return sg
}

func (sg *SymbolGraph) Contains(s string) bool {
	return sg.index[s] != 0
}

func (sg *SymbolGraph) Index(s string) int {
	return sg.index[s] - 1
}

func (sg *SymbolGraph) Name(v int) string {
	for key, val := range sg.index {
		if v == val - 1 {
			return key
		}
	}
	return ""
}

4.1.8 总结

基本概念：

  • 图的术语；
  • 图的表示方法；
  • 深度优先，广度优先；
  • 符号图。

4.2 有向图

在有向图种，边是单向的。

4.2.1 术语

  • 出度：指出的边的数量。
  • 头尾：第一个顶点称为头，第二个顶点称为尾。
  • 有向路径，有向环。
  • 简单有向环：不存在重复的顶点和边的环。

4.2.2 数据类型

有向图取反reverse()方法，返回有向图的一个副本，但所有的边方向反转。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
type Digraph struct {
	V int
	E int
	adj []Chapter01Foundation.ListBag
}

func NewDigraph(v int) *Digraph {
	return &Digraph{
		V: v,
		E: 0,
		adj: make([]Chapter01Foundation.ListBag, v),
	}
}

func (g *Digraph) AddEdge(v, w int) {
	g.adj[v].Add(w)
	g.E++
}

func (g *Digraph) Adj(v int) []interface{} {
	return g.adj[v].Iterator()
}

func (g *Digraph) Reverse() *Digraph {
	ret := NewDigraph(g.V)
	for v := 0; v < g.V; v++ {
		for _, row := range g.Adj(v) {
			w := row.(int)
			ret.AddEdge(w, v)
		}
	}
	return ret
}

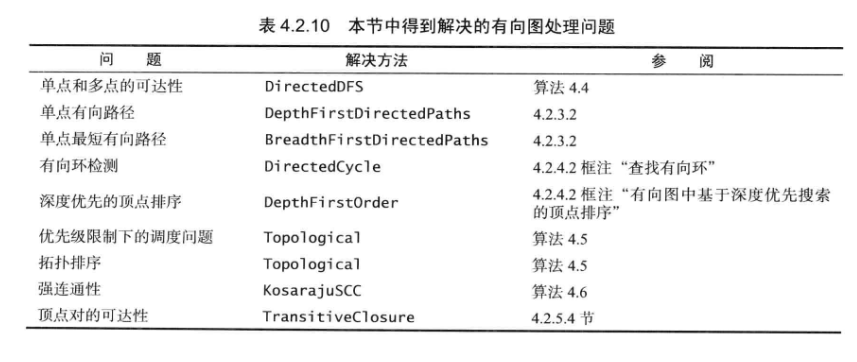
4.2.3 可达性

深度优先搜索。

有向图寻路：s -> v

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
type DirectedDFS struct {
	marked []bool
}

func NewDirectedDFS(g Graph, s int) *DirectedDFS {
	d := new(DirectedDFS)
	d.marked = make([]bool, g.V)
	d.DFS(g, s)
	return d
}

func (d *DirectedDFS) DFS(g Graph, v int) {
	d.marked[v] = true
	for _, w := range g.Adj(v) {
		if !d.marked[w.(int)] {
			d.DFS(g, w.(int))
		}
	}
}

4.2.4 环和有向无环图

处理优先级限制下的调度问题，有向图出现环会让调度进入循环。

寻找环：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
type DirectedCycle struct {
	marked []bool
	edgeTo []int
	cycle list.List
	onStack []bool
}

func NewDirectedCycle(g Graph) *DirectedCycle {
	ret := &DirectedCycle{
		onStack: make([]bool, g.V),
		edgeTo: make([]int, g.V),
		marked: make([]bool, g.V),
	}
	for v:=0; v < g.V; v++ {
		if !ret.marked[v] {
			ret.DFS(g, v)
		}
	}
	return ret
}

func (d *DirectedCycle) DFS(g Graph, v int) {
	d.onStack[v] = true
	d.marked[v] = true
	for _, row := range g.Adj(v) {
		w := row.(int)
		if d.HasCycle() {
			return
		} else if !d.marked[w] {
			d.edgeTo[w] = v
			d.DFS(g, w)
		} else if d.onStack[w] {
			d.cycle = list.New()
			for x:=v; x != w; x = d.edgeTo[x] {
				d.cycle.PushFront(x)
			}
			d.cycle.PushFront(w)
			d.cycle.PushFront(v)
		}
	}
}

func (d *DirectedCycle) HasCycle() bool {
	return d.cycle.Len() != 0
}

func (d *DirectedCycle) Cycle() list.List {
	return d.cycle
}

4.2.5 强连通性

如果两个顶点是相互可达的，称它们为强连通的。如果一幅图中任意两个顶点都是强连通的，则称这幅图是强连通的。

强连通分量：相互均为强连通的顶点的最大子集。

要另外实现一个取反操作才能进行。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
type KasarajuSCC struct {
	marked []bool
	id []int	//连通分量的编号
	count int	//当前编号
}

func NewKasarajuSCC(g Graph) *KasarajuSCC {
	ret := new(KasarajuSCC)
	ret.marked = make([]bool, g.V)
	ret.count = 0
	ret.id = make([]int, g.V)
	/*
	for s := 0; s < g.V; s++ {
		if !ret.marked[s] {
			ret.DFS(g, s)
			ret.count++
		}
	}
	*/
	return ret
}

func (cc *KasarajuSCC) DFS(g Graph, v int) {
	cc.marked[v] = true
	cc.id[v] = cc.count
	for _, wRow := range g.Adj(v) {
		w := wRow.(int)
		if !cc.marked[w] {
			cc.DFS(g, w)
		}
	}
}

func (cc *KasarajuSCC) StronglyConnected(v, w int) bool {
	return cc.id[v] == cc.id[w]
}

4.2.6 总结

4.3 最小生成树

加权图是为每条边关联一个权值或成本的图模型。

最小生成树是图的一棵含有其他所有顶点的无环连通子图。

最小生成树的两种经典算法：Prim算法和Kruskal算法。

4.3.1 原理

树的两个最重要的性质：

  • 用一条边连接树中的任意两个顶点会产生一个新的环；
  • 从树中删去一条边会得到两棵独立的树。

图的一种切分是将图的所有顶点分为两个非空且不重复的集合，横切边是一条连接两个属于不同集合的顶点的边。

切分定理：在一幅加权图中，给定任意的切分，它的横切边中权值最小者必然属于图的最小生成树。

切分定理是解决最小生成树问题的所有算法的基础。更确切地说，这些算法是贪心算法地特殊情况，使用切分定理找到一条边，不断重复直到找到最小生成树的所有边。

最小生成树的贪心算法：将V个顶点的任意加权连通图中属于最小生成树的边标记为黑色。初始状态下均为灰色，找到一种切分，它产生的横切边都不是黑色，将它权重最小的横切边标记为黑色。反复，直到标记V-1条黑色的边为止。

4.3.2 加权无向图的数据类型

带权重的边的数据类型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
type Edge struct {
	v, w int
	weight float64
}

func NewEdge(v, w int, wgh float64) *Edge {
	return &Edge{
		v: v,
		w: w,
		weight: wgh,
	}
}

func (e *Edge) Either() int {
	return e.v
}

func (e *Edge) Other(v int) int {
	if v == e.v {
		return e.w
	}
	if v == e.w {
		return e.v
	}
	return -1
}

func (e *Edge) CmpTo(that Edge) int {
	if e.weight > that.weight {
		return 1
	}
	if e.weight < that.weight {
		return -1
	}
	return 0
}

加权无向图的数据类型：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
type EdgeWeightedGraph struct {
	V int
	E int
	adj []Chapter01Foundation.ListBag
}

func NewEdgeWeightedGraph(v int) *EdgeWeightedGraph {
	return &EdgeWeightedGraph{
		V: v,
		E: 0,
		adj: make([]Chapter01Foundation.ListBag, v),
	}
}

func (g *EdgeWeightedGraph) AddEdge(e Edge) {
	v, w := e.v, e.w
	g.adj[v].Add(e)
	g.adj[w].Add(e)
	g.E++
}

4.3.3 最小生成树API

edges()返回最小生成树的所有边。

weigh()返回最小生成树的权重。

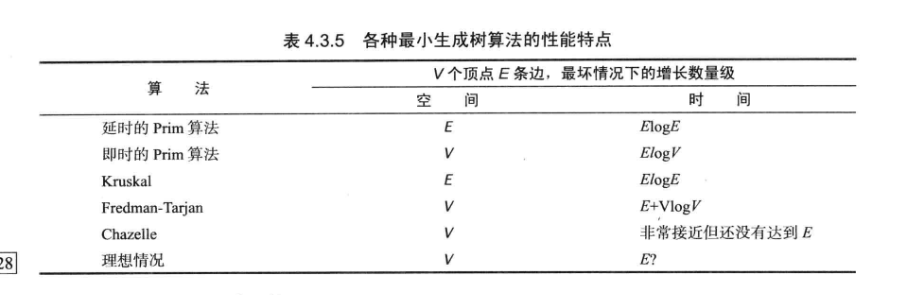
4.3.4 Prim算法

每一步都会为一棵生长中的树添加一条边。一开始这棵树只有一个顶点，然后添加V-1条边，每次总是将下一条连接树中的顶点与不在树中的顶点且权值最小的边加入树中。

最小生成树的Prim算法的延时实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
type LazyPrimMST struct {
	marked []bool	// 顶点
	mst *Chapter01Foundation.ListQueue  // 边
	// 横切边，原文是最小队列，我是最大队列
	//pq *Chapter02Sorting.MaxPriorityQueue
	pq *list.List
}

func (p *LazyPrimMST) Visit(g EdgeWeightedGraph, v int) {
	p.marked[v] = true
	for _, row := range g.Adj(v) {
		e := row.(Edge)
		if !p.marked[e.Other(v)] {
			p.pq.PushFront(e)
			p.SortList()
		}
	}
}

func (p *LazyPrimMST) SortList() {
	if p.pq.Len() == 0 {
		return 
	}
	min := p.pq.Front()
	for po := p.pq.Front(); po != nil; po = po.Next() {
		if po.Value.(Edge).weight < min.Value.(Edge).weight {
			min = po
		}
	}
	p.pq.MoveBefore(min, p.pq.Front())
}

func NewLazyPrimMST(g EdgeWeightedGraph) *LazyPrimMST {
	ret := new(LazyPrimMST)
	ret.pq = list.New()
	ret.marked = make([]bool, g.V)
	ret.mst = new(Chapter01Foundation.ListQueue)
	ret.Visit(g, 0)
	for ret.pq.Len() != 0 {
		e := ret.pq.Remove(ret.pq.Front()).(Edge)
		ret.SortList()
		v := e.Either()
		w := e.Other(v)
		if ret.marked[v] && ret.marked[w] {
			continue
		}
		ret.mst.Enqueue(e)
		if !ret.marked[v] {
			ret.Visit(g, v)
		}
		if !ret.marked[w] {
			ret.Visit(g, w)
		}
	}
	return ret
}

4.3.5 Prim算法的即时实现

不需要保存所有的边，只需要保存权值最小的边，只会在优先队列保存每个非树顶点w的一条边，这条边是与树中顶点连接起来的权值最小的边。

4.3.6 Kruskal算法

按照权值顺序处理它们，将边加入最小生成树中，加入的表不会构成环，直到加入V-1条边。

4.3.7 展望

4.4 最短路径

最短路径是权重最小者。

4.4.1 性质

  • 路径是有向的。
  • 权重不一定等价于距离，可能是时间等。
  • 并不是所有顶点都是可达的，为了简化问题，假设都是强连通的。
  • 最短路径不一定是唯一的，但是只需要找到一条就行。
  • 最短路径树：以s为起点，包含s和从s可达的所有顶点。

4.4.2 加权有向图的数据结构

加权有向边的数据类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
type DirectedEdge struct {
	v int
	w int
	weight float64
}

func NewDirectedEdge(v, w int, weight float64) *DirectedEdge {
	return &DirectedEdge{v, w, weight}
}

func (E *DirectedEdge) From() int {
	return E.v
}

func (E *DirectedEdge) To() int {
	return E.w
}

加权有向图的数据类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
type EdgeWeightedDigraph struct {
	V int
	E int
	adj []list.List
}

func NewEdgeWeightedDigraph(v int) *EdgeWeightedDigraph {
	return &EdgeWeightedDigraph{v, 0, make([]list.List, v)}
}

func (dg *EdgeWeightedDigraph) AddEdge(e DirectedEdge) {
	dg.adj[e.From()].PushFront(e)
	dg.E++
}

func (dg *EdgeWeightedDigraph) Adj(v int) *list.List {
	return &dg.adj[v]
}

func (dg *EdgeWeightedDigraph) Edges() *list.List {
	ret := list.New()
	for v := 0; v < dg.V; v++ {
		l := dg.adj[v]
		for tmp := l.Front(); tmp != nil; tmp = tmp.Next() {
			ret.PushBack(tmp.Value)
		}
	}
	return ret
}

4.4.3 理论基础

最短路径的最优性条件。

4.4.4 Dijkstra算法

4.4.5 无环加权有向图的最短路径算法

4.4.6 一般加权有向图的最短路径问题

4.4.7 展望